glTF-Tutorials

Previous: Simple Animation Table of Contents Next: Simple Meshes

Animations

As shown in the Simple Animation example, an animation can be used to describe how the translation, rotation, or scale properties of nodes change over time.

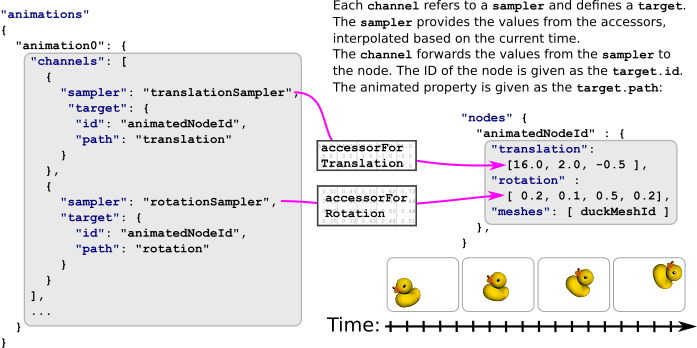
The following is another example of an animation. This time, the animation contains two channels. One animates the translation, and the other animates the rotation of a node:

  "animations": [
    {
      "samplers" : [
        {
          "input" : 2,
          "interpolation" : "LINEAR",
          "output" : 3
        },
        {
          "input" : 2,
          "interpolation" : "LINEAR",
          "output" : 4
        }
      ],
      "channels" : [ 
        {
          "sampler" : 0,
          "target" : {
            "node" : 0,
            "path" : "rotation"
          }
        },
        {
          "sampler" : 1,
          "target" : {
            "node" : 0,
            "path" : "translation"
          }
        } 
      ]
    }
  ],

Animation samplers

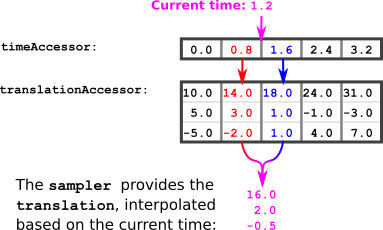
The samplers array contains animation.sampler objects that define how the values that are provided by the accessors have to be interpolated between the key frames, as shown in Image 7a.


Image 7a: Animation samplers.

In order to compute the value of the translation for the current animation time, the following algorithm can be used:

Example:

Imagine the currentTime is 1.2. The next smaller element from the times accessor is 0.8. The next larger element is 1.6. So

previousTime = 0.8
nextTime     = 1.6

The corresponding values from the translations accessor can be looked up:

previousTranslation = (14.0, 3.0, -2.0)
nextTranslation     = (18.0, 1.0,  1.0)

The interpolation value can be computed:

interpolationValue = (currentTime - previousTime) / (nextTime - previousTime)
                   = (1.2 - 0.8) / (1.6 - 0.8)
                   = 0.4 / 0.8         
                   = 0.5

From the interpolation value, the current translation can be computed:

currentTranslation = previousTranslation + interpolationValue * (nextTranslation - previousTranslation)
                   = (14.0, 3.0, -2.0) + 0.5 * ( (18.0, 1.0,  1.0) - (14.0, 3.0, -2.0) )
                   = (14.0, 3.0, -2.0) + 0.5 * (4.0, -2.0, 3.0)
                   = (16.0, 2.0, -0.5)

So when the current time is 1.2, then the translation of the node is (16.0, 2.0, -0.5).

Animation channels

The animations contain an array of animation.channel objects. The channels establish the connection between the input, which is the value that is computed from the sampler, and the output, which is the animated node property. Therefore, each channel refers to one sampler, using the index of the sampler, and contains an animation.channel.target. The target refers to a node, using the index of the node, and contains a path that defines the property of the node that should be animated. The value from the sampler will be written into this property.

In the example above, there are two channels for the animation. Both refer to the same node. The path of the first channel refers to the translation of the node, and the path of the second channel refers to the rotation of the node. So all objects (meshes) that are attached to the node will be translated and rotated by the animation, as shown in Image 7b.


Image 7b: Animation channels.

Interpolation

The above example only covers LINEAR interpolation. Animations in a glTF asset can use three interpolation modes :

Step

The STEP interpolation is not really an interpolation mode, it makes objects jump from keyframe to keyframe without any sort of interpolation. When a sampler defines a step interpolation, just apply the transformation from the keyframe corresponding to previousTime.

Linear

Linear interpolation exactly corresponds to the above example. The general case is :

Calculate the interpolationValue:

    interpolationValue = (currentTime - previousTime) / (nextTime - previousTime)

For scalar and vector types, use a linear interpolation (generally called lerp in mathematics libraries). Here’s a “pseudo code” implementation for reference

    Point lerp(previousPoint, nextPoint, interpolationValue)
        return previousPoint + interpolationValue * (nextPoint - previousPoint)

In the case of rotations expressed as quaternions, you need to perform a spherical linear interpolation (slerp) between the previous and next values:

    Quat slerp(previousQuat, nextQuat, interpolationValue)
        var dotProduct = dot(previousQuat, nextQuat)
        
        //make sure we take the shortest path in case dot Product is negative
        if(dotProduct < 0.0)
            nextQuat = -nextQuat
            dotProduct = -dotProduct
            
        //if the two quaternions are too close to each other, just linear interpolate between the 4D vector
        if(dotProduct > 0.9995)
            return normalize(previousQuat + interpolationValue(nextQuat - previousQuat))

        //perform the spherical linear interpolation
        var theta_0 = acos(dotProduct)
        var theta = interpolationValue * theta_0
        var sin_theta = sin(theta)
        var sin_theta_0 = sin(theta_0)
        
        var scalePreviousQuat = cos(theta) - dotproduct * sin_theta / sin_theta_0
        var scaleNextQuat = sin_theta / sin_theta_0
        return scalePreviousQuat * previousQuat + scaleNextQuat * nextQuat

This example implementation is inspired from this Wikipedia article

Cubic Spline interpolation

Cubic spline interpolation needs more data than just the previous and next keyframe time and values, it also need for each keyframe a couple of tangent vectors that act to smooth out the curve around the keyframe points.

These tangent are stored in the animation channel. For each keyframe described by the animation sampler, the animation channel contains 3 elements :

The input and output tangents are normalized vectors that will need to be scaled by the duration of the keyframe, we call that the deltaTime

     deltaTime = nextTime - previousTime

To calculate the value for currentTime, you will need to fetch from the animation channel :

note: the input tangent of the first keyframe and the output tangent of the last keyframe are totally ignored

To calculate the actual tangents of the keyframe, you need to multiply the direction vectors you got from the channel by deltaTime

    previousTangent = deltaTime * previousOutputTangent
    nextTangent = deltaTime * nextInputTangent

The mathematical function is described in the Appendix C of the glTF 2.0 specification.

Here’s a corresponding pseudocode snippet :

    Point cubicSpline(previousPoint, previousTangent, nextPoint, nextTangent, interpolationValue)
        t = interpolationValue
        t2 = t * t
        t3 = t2 * t
        
        return (2 * t3 - 3 * t2 + 1) * previousPoint + (t3 - 2 * t2 + t) * previousTangent + (-2 * t3 + 3 * t2) * nextPoint + (t3 - t2) * nextTangent;
Previous: Simple Animation Table of Contents Next: Simple Meshes
This site is open source. Improve this page.